Jaehyeon

Heo

(Teddy)

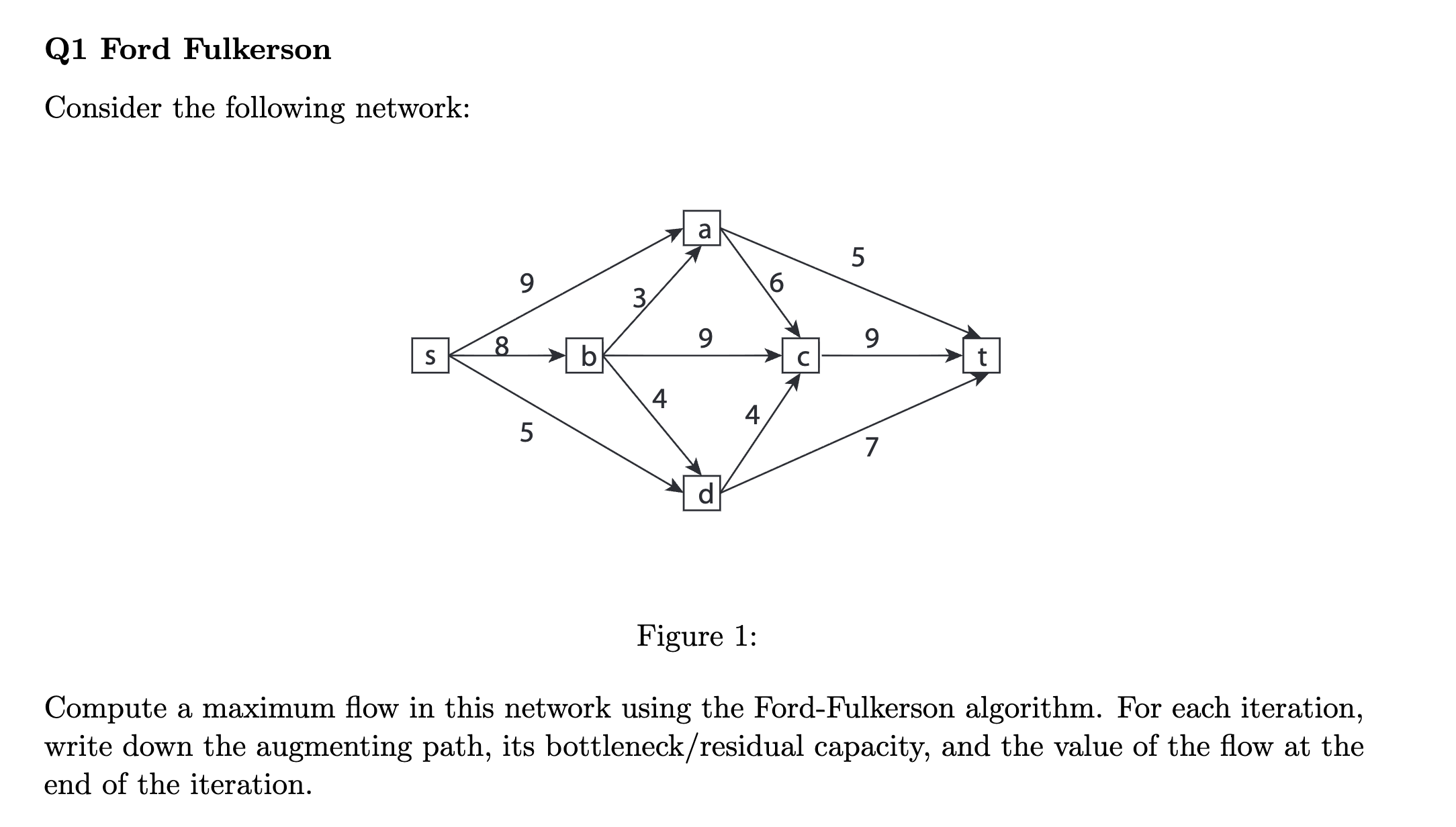
Initial Residual Network $G_f$ for initial $f$ (0 assignment)

Iteration	Augmenting Path	Bottleneck $\Delta$	Flow Value
1	$s \rightarrow a \rightarrow c \rightarrow t$	$6$	$6$
2	$s \rightarrow b \rightarrow a \rightarrow t$	$3$	$9$
3	$s \rightarrow b \rightarrow c \rightarrow t$	$3$	$12$
4	$s \rightarrow b \rightarrow d \rightarrow t$	$2$	$14$
5	$s \rightarrow a \rightarrow t$	$2$	$16$
6	$s \rightarrow d \rightarrow t$	$5$	$21$

Interactive Walkthrough

We can now notice that all the edges going into vertex $t$ has capacity $0$, so we know for sure that no more simple path exists from $s$ to $t$.